I am an applied mathematician primarily interested in real-life problems whose treatment requires analysis of a model / justification of the approximation or those that can be effectively tackled with analytical tools such as asymptotic methods or closed-form solution reducibility.
I enjoy learning new things while working on diverse subjects analysing a problem, devising a constructive solution approach and verifying / implementing it numerically. Current and past topics of my research include:
- wave propagation in porous media (fluid / solid inclusion scattering for Biot elastodynamics equations);
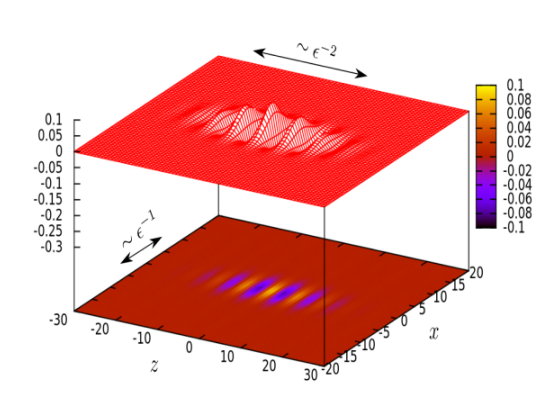
- nonlinear PDEs (analysis of one NLS model for laser beams in photopolymers; Darboux transformation);
- approximation theory (approximation of square-integrable functions by traces of analytic functions with certain properties such as pointwise constraints);
- integral equations and optimal bases construction (spectral theory for compact one-dimensional self-adjoint integral operators with convolution kernels);
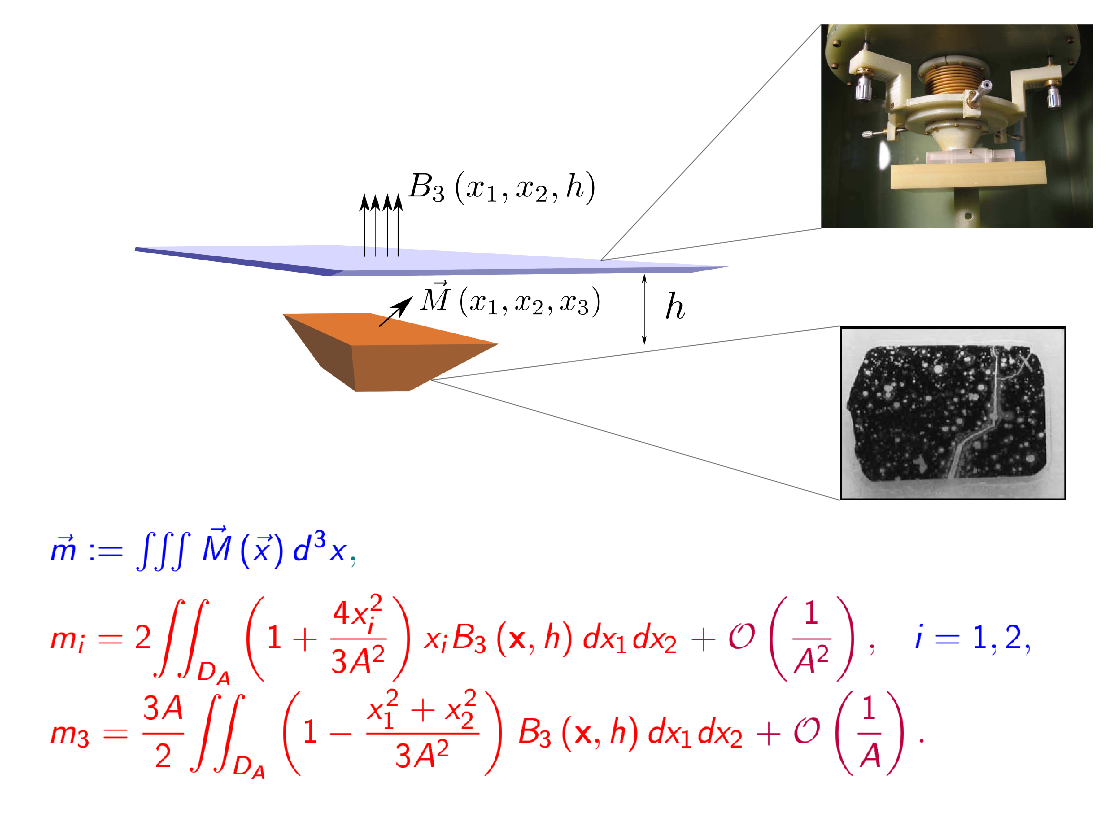
- inverse magnetisation problem (analytical estimation of net magnetisation moment components from partial measurements of magnetic field);
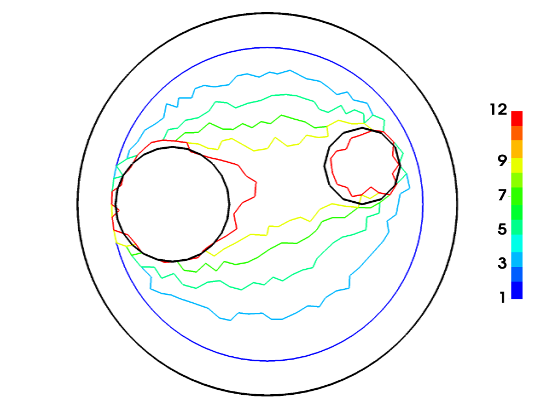
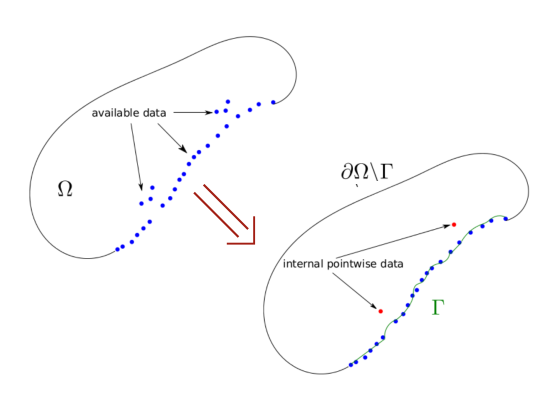
- inverse obstacle problem (determining domain geometry for transient wave equation from partial Dirichlet+Neumann data);
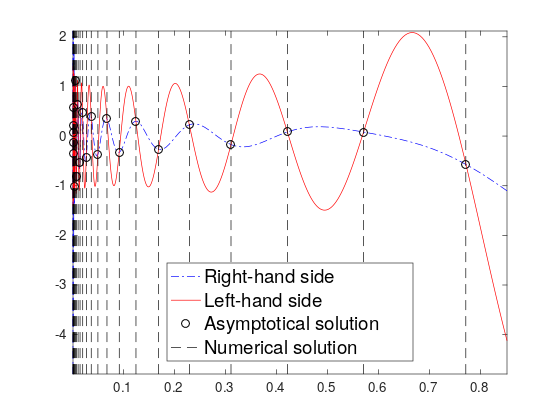
- efficient solution of the Helmholtz equation (asymptotic-numerical methods for high-frequency wave propagation in homogeneous and heterogeneous media);
- long-time behaviour analysis for solutions of wave equations (extension of the limiting amplitude principle and decay problems in unbounded domains);
- contact-mechanical problems (integral equation approach; development, solution and analysis of a new model for wear in the punch-sliding problem).
Before that, I did my "specialist" program at Moscow Engineering Physics Institute MEPhI (Faculty of Theoretical and Experimental Physics), Russia, followed by 2 M.Sc. degrees: from the international EU Erasmus Mundus program MathMods (now InterMaths) in 2010, and McMaster University (Department of Mathematics & Statistics), Canada, in 2012, with a M.Sc. thesis work on the analysis of nonlinear wave propagation in photopolymers written under supervision of Dmitry Pelinovsky.
After my Ph.D., from 2016 to 2018, I was a post-doc at ENSTA Paris (France) working with Laurent Bourgeois on the inverse obstacle problem for the time-domain wave equation with constant coefficients.
Since 2018, I have been employed by Institute of Analysis & Scientific Computing at Technical University of Vienna (TU Wien), Austria, as a research postdoc, working in the group of Anton Arnold (in collaboration with Ilaria Perugia and Sjoerd Geevers from University of Vienna), on different aspects of linear wave propagation.
In 2022, I have been on a partial teaching contract at TU Wien, see the "Teaching" section for more details.
From 2019 to 2024, I was also affiliated with the St. Petersburg Department of Steklov Mathematical Institute of Russian Academy of Sciences as a permanent researcher on unpaid leave.
Since October 2022, I hold ISFP (Inria Starting Faculty Position) at Centre Inria d'Université Côte d'Azur as a member of the FACTAS research team working on inverse problems.
You can contact me by email: dmvpon@gmail.com / dmitry.ponomarev@inria.fr, or find me at:
Office B.222, FACTAS team,
Centre Inria d'Université Côte d'Azur,
2004 Route des Lucioles, 06902 Biot, France.